IM® K–5 Math + Fluency
Supporting Fluency Development with IM K–5 Math
Based on research and advice from expert educators and mathematicians, IM approached fluency through a coherent progression of skills integrated throughout the IM K–5 Math curriculum. Fluency is an ongoing goal that is developed, practiced, and reinforced across every activity and lesson.
As students solve problems and compare approaches, they refine efficient strategies that build automaticity alongside deep conceptual understanding.
In this video, former lead writer Dionne Aminata shares the intentional design of the curriculum and students show their accuracy, efficiency, and flexibility with math facts.
Download our Fluency Development e-book, and use it as a resource to support students’ confidence in their execution of skills with a purpose.
Ready to get started with IM K–5 Math?
In IM K–5 Math, fluency means:
In IM K–5 Math, fluency is built:
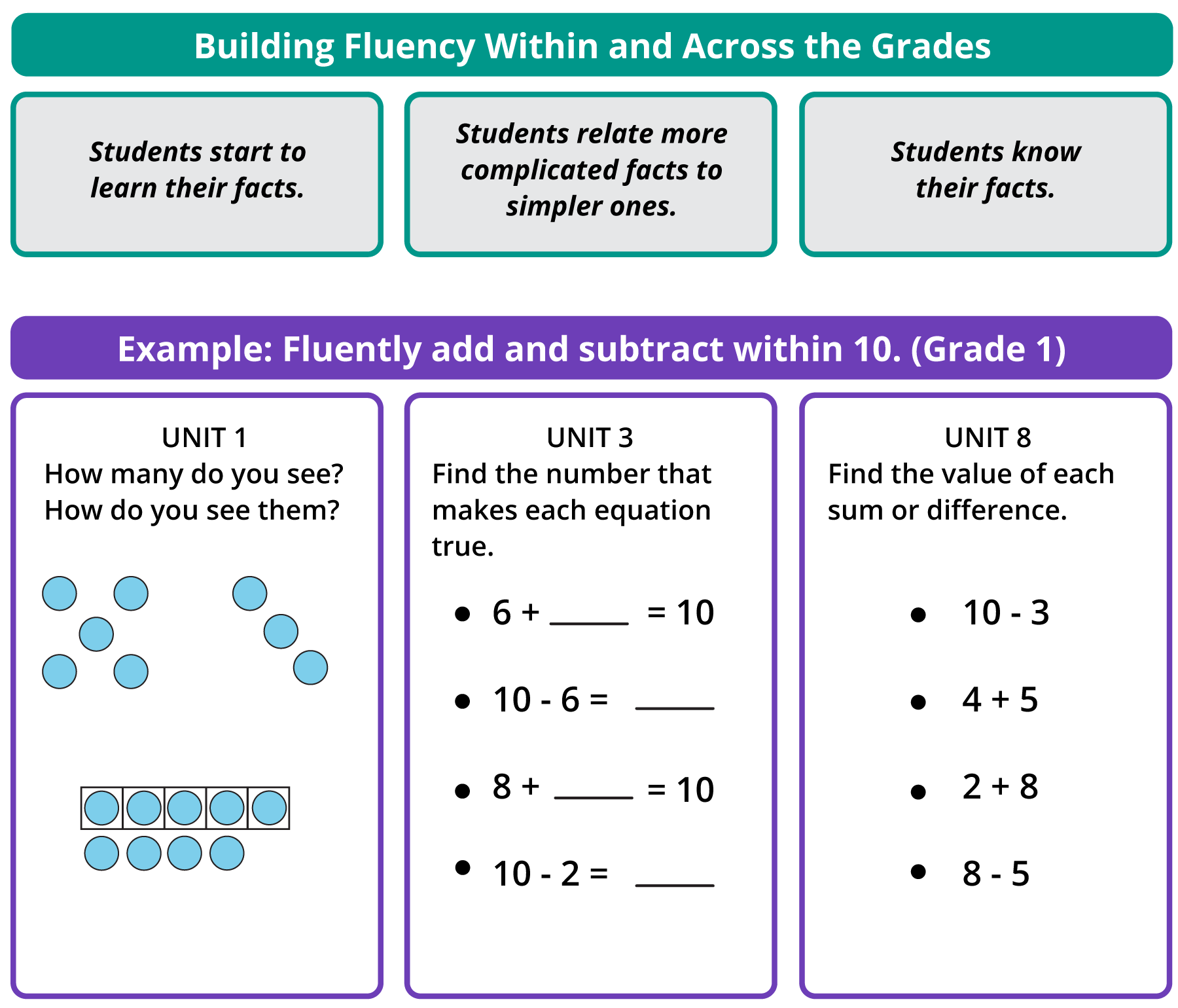
- across the units through a sequence of learning goals that make sense to the learner
- across the year through conceptual understanding and by connecting the relevant standards through a coherent story within and across units and centers
- across the grades through the representations, strategies, and algorithms
In IM K-5 Math, fluency is built within and across grades:
Centers afford students opportunities to practice by recalling facts, computing mentally, and writing true equations. In the examples that follow, students work with either cubes or number cards to make 10 with one part given. As students share their thinking and write the equations, they begin to learn new facts.
How teachers can use IM K–5 Math to gauge fluency:
Teachers can use monitoring sheets, which are aligned to section and unit goals, and End-of-Unit assessments to track student progress towards math fluency over the course of the year.
What is fluency?
“Procedural fluency refers to knowledge of procedures, knowledge of when and how to use them appropriately, and skill in performing them flexibly, accurately, and efficiently,” as defined in Adding It Up: Helping Children Learn Mathematics from the National Research Council (2001).
What is IM’s stance on mathematics fluency in K–5 curriculum?
IM K–5 Math is designed so that students build procedural fluency and conceptual understanding simultaneously. The representations, strategies, and algorithms that are used and highlighted are purposefully designed for coherence. Fluency is embedded throughout the lessons, rather than isolated as a separate skill.
How does the fluency practice embedded in IM K–5 Math support teachers in meeting the needs of all students?
Teachers can use what they know about their students’ backgrounds, strengths, and ways of making meaning to create meaningful opportunities for developing and practicing fluency. The instructional routines and centers in our materials offer collaborative, community-oriented ways for students to learn and practice math facts.
Lesson activities and centers also give students chances to reflect on their progress by identifying the facts they already know and the facts they are working on. This reflection supports goal-setting and helps students take an active role in their own fluency development.
How does IM K–5 Math reinforce fluency with facts?
Students are given opportunities throughout the year to name the facts they know, the facts they are still learning, and identify strategies to learn these facts. Warm-up routines, such as Number Talks and True or False, plus centers and games during lessons support students in becoming more fluent throughout the year.
How do learners gain fluency through the centers?
The centers, which are usually activities or games, are designed in stages. The stages are often broken down by ranges of numbers that students are operating with so teachers can systematically support students with stages based on the facts they need to practice.
Centers are meant for extra practice in school or outside of school and are designed to build fluency (or any skill that develops over time) across a year.
Centers:
- are aligned to grade levels and units
- consist of stages with the same general structure
- can be repeated with different results each time
- primarily focus on the major work of grade
What does it look like for a student to know math from memory, in terms of timed tests?
Illustrative Mathematics does not take a position on timed tests for assessing students’ knowledge of math. Assessment can be conducted in various ways and is not limited to timed tests. For example, assessment also includes a teacher engaging with students and observing students while walking around the classroom.
How does a student demonstrate fluency?
A student who is fluent in mathematics can flexibly, efficiently, and accurately use computational methods. For example, a student fluent in addition computation can mentally use 10 + 5 = 15 to know that 9 + 6 = 15.
I want further information on the topic of fluency. What resources are available?
- National Council of Teachers of Mathematics. (2000). Principles and Standards for School Mathematics. Reston, VA: NCTM.
- Kilpatrick, J., Swafford, J., & Findell, B. (2001). Adding It Up: Helping Children Learn Mathematics. Washington, DC: National Academy Press.
Featured IM K–5 Math Fluency Blog Posts
